This is a note on the control part of the article Design and Control of a Soft and Continuously Deformable 2D Robotic Manipulation System. In this paper the authors described the design, fabrication, control, and experimental validation of a soft and highly compliant 2D manipulator.
Curvature Estimation
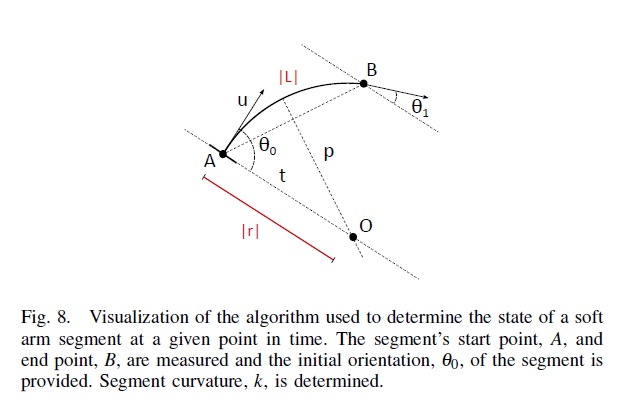
In order to control the pose of arbitrary points along the soft robot arm in task space, it is first necessary to estimate an arm segment’s state in arc space using available localization data.
PCC Assumption: assume the state of an arm segment can be represented by a signed curvature $k$ and knowledge of its starting orientation $\theta_0$.
Forward Kinematics
The orientation at any point $s\in[0,~L_i]$ along the arc representing segment $i$ within a chain of $n$ segments composing the arm can be expressed as:
\[\theta_i(s) = k_i s+\theta_i(0)\]Assume $\theta_i(0) = \theta_{i-1}(L_{i-1})$ (because segments are serially connected and continuous)
Position of any point along the arm
\[\begin{align} x_i(s) &= x_{i-1}(L_{i-1})+\int_0^s \cos[\theta_i(s')]ds'\\ y_i(s) &= x_{i-1}(L_{i-1})+\int_0^s \sin[\theta_i(s')]ds'\\ \end{align}\]Inverse Kinematics Algorithm
Objective: Determine a small update to segment curvatures that will move a controlled point or points towards desired pose $\vec{w}_d=[x_d,~y_d,~\theta_d]$
Each iteration, the algorithm calculates the incremental curvature updates $\Delta k$. Upon completion, return the curvatures required to attain the desired arm pose at that control time step.
Approach: Iterative Jacobian transpose approach
\[J=\frac{\partial\vec{w}\left(\vec{L},~\vec{k}, \theta_0(0)\right)}{\partial\vec{k}}\]Main Control Algorithm
Objective: Determine adjustments to segment curvatures in real-time that are required to move a point or points along the arm through their requested pose trajectory.
Pass the computed required curvature updates to the lower level segment controllers.
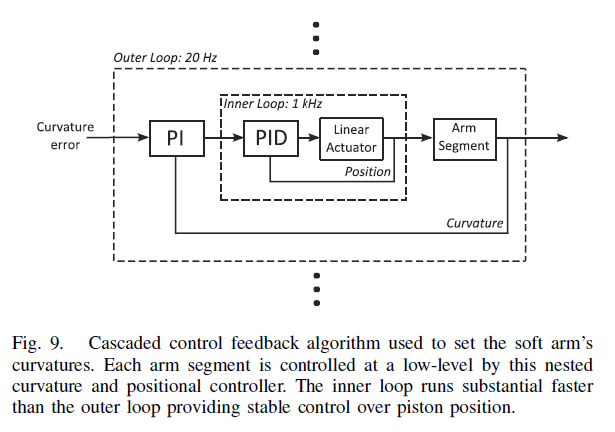
Arm Segment Controller
This low-level control algorithm periodically receives discrepancies between the soft arm’s measured and requested curvatures and uses a cascaded control structure to effectively adjust fluidic drive cylinders and resolve the error.
The controller achieves this by running a PI computation on the curvature error in order to generate a new set-point for the positional control of the linear actuator.
Outer Loop
- Relatively slow rate
- Initiated when the main control algorithm produces a curvature error
Inner Loop
- Positional PID controller
- Bring the cylinder’s piston displacement (fluid pressure) to the newly determined set-point



Comments powered by Disqus.